Last October, Zerosync's Robin Linus dropped a bomb in the form of BitVM. One of the longest-standing criticisms of Bitcoin is that it is not possible to create arbitrary programs to control how funds are spent or locked. Bitcoin has very limited programmability in its scripting language, and the primitives available are very limited. You can verify the signature, you can add a time lock to something, you can manipulate the data in many simple ways, but that's it.
You can program Bitcoin UTXO to require signature verification, time lock verification, etc. But you can't program it to open based on any arbitrary conditions. Robin's vision with BitVM was that one rudiment in computing could It is enforced in the Bitcoin script: a NAND gate, a fundamental primitive of computing at the physical/electrical level. Every possible computation can be generated from NAND gates.
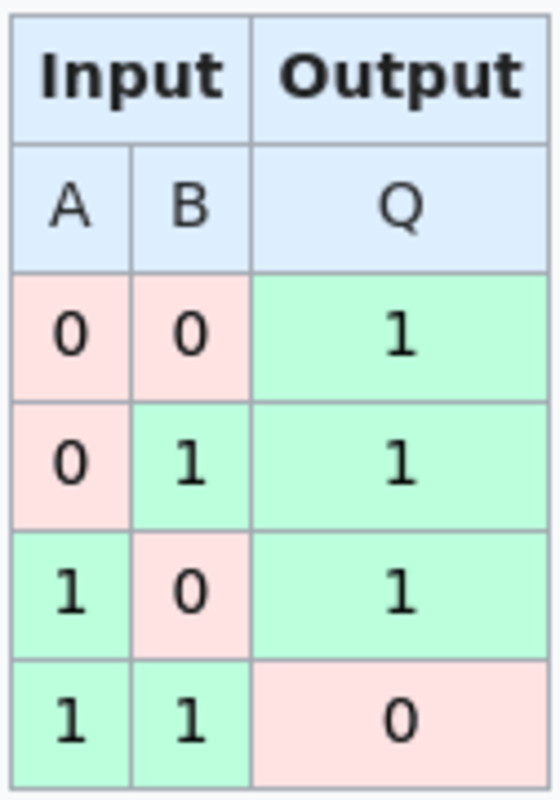
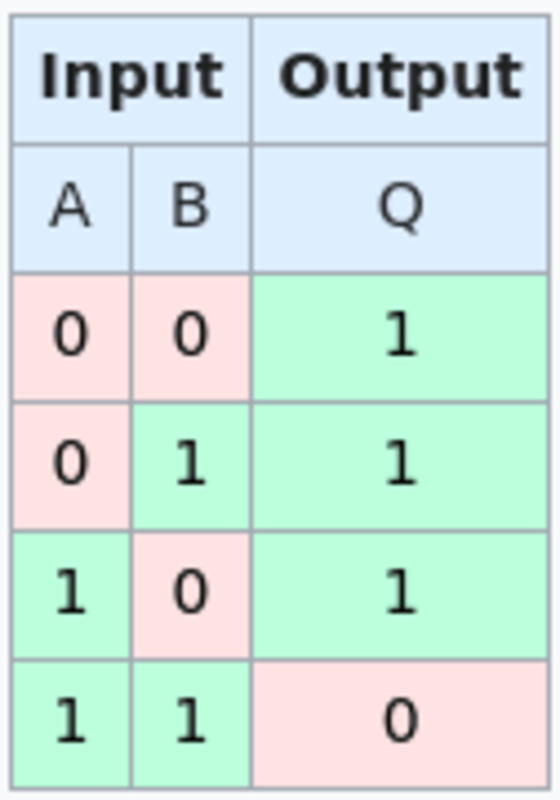
The script can actually check the NAND gate thanks to a neat trick with OP_BOOLAND and OP_NOT. OP_BOOLAND is an AND operation, which is the opposite of a NAND operation. OP_NOT takes a binary value of 1 or 0 and inverts it. Together, this allows you to implement a single NAND operation directly in the script. In combination with hashing, a NAND gate script can be created where each input and output field contains a potential hash to “unlock” this spending path, each one pushing a 1 or 0 onto the stack to perform a NAND operation. Each script also has a path through which you can expose it both of them Raw images to one bit value, you can claim money instantly. This is because once someone decides what to input into a NAND gate, they cannot change their mind without losing money.
An enormous amount of NAND gate text can be compressed into a root tree, and once one person commits bit values off-chain for input into that computation, the other party can challenge them on any individual step in the computation to prove that it is being executed correctly on-chain. Each “challenge” allows the challenging party to prove that the individual gate has been calculated correctly, otherwise the other party can claim the funds after a specified period of time. By going back and forth in this way if the account is disputed, it is certain that the cheating party will eventually be caught and lose the money.
Restrictions
The main limitation of BitVM is that only people involved in creating BitVM nodes can participate, and the roles are very limited. There is the prover, the person who confirms how the off-chain computation occurred, and the verifier, the person who can challenge the computation and force it to be proven on-chain if the prover does not complete the off-chain computation or tries to lie about the results
One of the reasons for designing BitVM was to create two-way connectivity to sidechains or other systems. The scheme offers a very powerful primitive in this use case, which is the ability to actually enforce funds to one party or another based on the validity of an arbitrary calculation, i.e. validating whether a bigot is valid according to the rules of sidechains. The problem is that only people who hold BitVM UTXO keys can say “Hey, you're cheating!” When someone, engage in a challenge protocol. This ultimately makes the system still reliable.
Another limitation is that the challenge response protocol can be very long. If someone realizes that the result of the calculation will result in them losing money and stops responding, the proofreader must essentially guess where the single NAND gate is located in the calculation which the proofreader must lie to and expose both first images to the thing that would give the validator money. Until that particular gate on the chain is challenged, the installer can still properly respond to the challenge and pull it out. This can be time consuming and ineffective.
Some improvements have been made to this design since the original proposal to allow multiple validators to be in the system with the prover, to create a 1-of-n trust model where only one validator is needed to challenge the dishonest prover. However, this requires creating multiple BitVM instances in parallel to accomplish, thus increasing the shortcomings of the original design for both parties.
Pete VM2
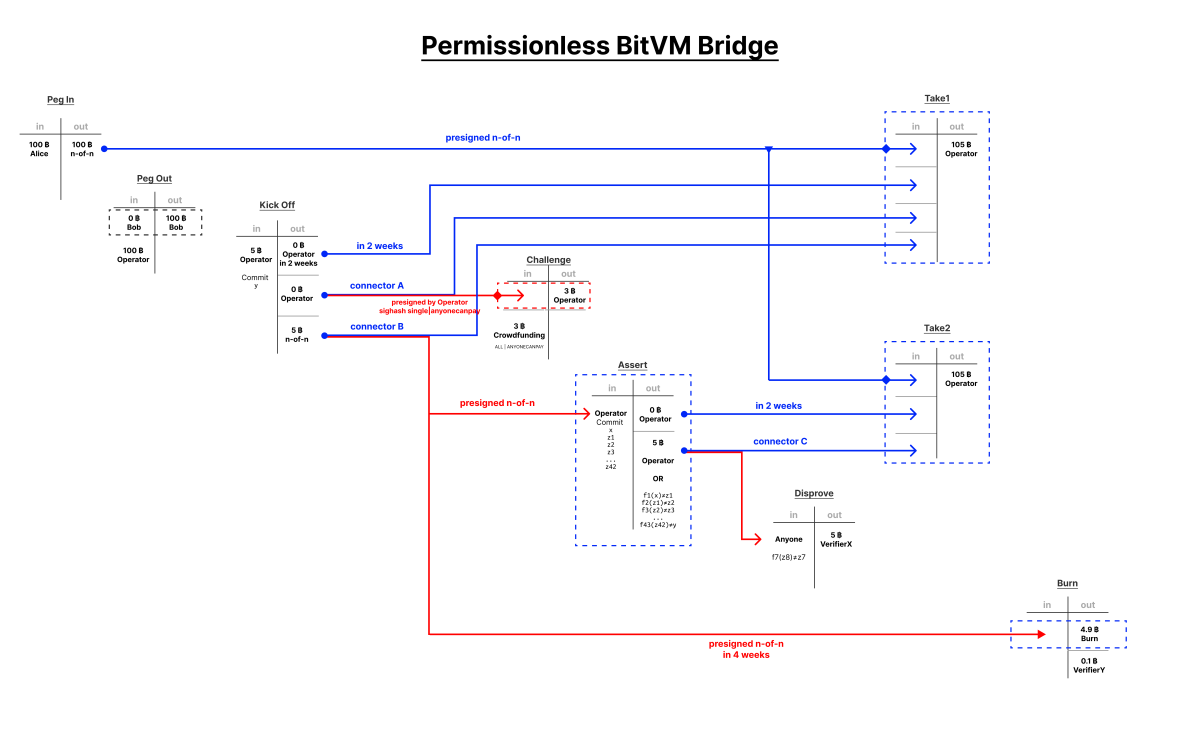
Robin recently proposed a design scheme for BitVM 2. This scheme seeks to make some compromises compared to the original design in the interest of mitigating its major drawbacks. BitVM 2 shortens the length of the challenge/response protocol from an indefinite series of transactions that can reach dozens in a worst-case scenario, to two rounds in a challenge/response. In addition, it allows the use of connector outputs anyone To work as an auditor. It does not require someone to be a member involved in the creation of BitVM to challenge a dishonest installer.
The key shift here is to move away from directly using text NAND gates to directly implement the primitive arithmetic trace, and move to using them to implement the general zero-knowledge proof-of-knowledge verifier SNARK (one of the core primitives that Rubin intended from the beginning to implement with BitVM). Instead of putting the raw inputs into the raw computation trace, and running it gate by gate in their Tapleaf scripts, the BitVM 2 instance's input will simply be zero-knowledge proof inputs with computation-assured outputs.
In addition to abstracting the computation implementation using ZKP, tabliff scripts are greatly expanded from a single NAND gate per sheet to a complete subfunction of the ZKP checker. Instead of the challenge response protocol relying on the verifier guessing at which NAND gate the installer attempted to cheat, and selectively challenging at one gate, the verifier could prove that the output of the entire subfunction is invalid based on the input.
Just like BitVM 1, contracts are pre-negotiated using pre-signed transactions and fork scripts. The funds associated with BitVM are sent to an n-of-n multisig that signs two possible execution transactions, one in which no challenge occurs, and one in which a challenge occurs. To begin the contract execution process, the installer initiates the start transaction. This starting transaction commits to the output value “y” that they claim the computation produces, and includes three outputs: a timed output that is included in the non-challenge execution transaction, connector A output, and connector B output, both of which are also spent in the non-challenge transaction.
This is where the design allows anyone to participate as a validator. Connector A's output has a second pre-signed transaction that it can spend, which is the challenge transaction. This is a pre-signed transaction that pays the installer a bond in Bitcoin, but the output of connector A is not enough to fund it. Literally anyone can add their own input to fund the transaction and spend Connector A's output, invalidating the withdrawal transaction without challenging the installer (there is one input that does not need to be challenged).
This imposes a challenging path. The output of Connector B can also be spent using a pre-signed transaction, the Confirm Transaction, to output each sub-job in the entire BitVM 2 contract. This requires a large transaction with a lot of data, but remember that the final “y” that the proverb claims is the resulting computation has already been committed in the initial transaction. This creates two exits. One is a time-locked output, and the other is a C-connector output. Each of these outputs, plus the original tied funds, are spent on the installer's second successful withdrawal transaction after the time lock.
The outputs of connector C can also be used by anyone who can prove that any subfunction outputs on BitVM 2 nodes produce invalid outputs. This requires a very large transaction, because the script needed to prove that an entire section of a BitVM account is invalid is huge, but in this single transaction the validator can claim the coins on the connector's output with valid proof. This invalidates the installer's second withdrawal transaction and effectively burns the coins. The only way to get it back at this point is if the proverbial and everyone All investigators collaborate to fund the original n-of-n multisig to restore it. Connector B's exit in the starting transaction can also be spent after a much longer delay than the non-challenge has been withdrawn to invalidate both the non-challenge and the confirmation transaction, burning the staked coins.
This reduces what would have been a ridiculous series of transactions in BitVM's original proposal to force the correct contract outcome, to a maximum of four transactions (although they are very large transactions), while in the process creating a validator set for a BitVM 2 instance literally i.e. Someone with Bitcoin who will fund the challenge transaction.
BitVM 2 may end up being a major breakthrough in terms of the wave of colocation and other layer 2 pools that aim to use BitVM as a two-way backhaul. The pool operator (installed in BitVM) can use its own funds to cover the withdrawals of users they have linked to the system, and periodically withdraw these funds from BitVM to compensate themselves. any The user or interested party will then be able to punish them by burning their funds if they can provide evidence that the operator was not processing all withdrawals correctly.
It is important to note that ultimately the security of a BitVM 2 instance is backed by the n-of-n key holder, although people who are not involved in it can still challenge the installer as a validator. But since the validator has an efficient exit in the absence of competitors, and anyone funding a challenge transaction can act as a validator, an n-of-n multi-funding can follow a setup and key deletion ceremony similar to launching Zcash to improve its security.
BitVM 2 will likely end up being a major breakthrough in terms of improving the resiliency and trust model of two-way connectivity that uses BitVM. Once again, Robin proved that he is a true magician.